Gerak Lurus Beraturan

Apa itu Gerak lurus beraturan??

Gerak lurus beraturan didefinisikan sebagai gerak suatu benda dengan kecepatan tetap. Kecepatan tetap artinya baik besar maupun arahnya tetap. Kecepatan tetap yaitu benda menempuh jarak yang sama untuk selang waktu yang sama. Misalnya sebuah mobil bergerak dengan kecepatan tetap 75 km/jsm atau 1,25 km/menit, berarti setiap menit mobil itu menempuh jarak 1,25 km. Karena kecepatan benda tetap, maka kata kecepatan pada gerak lurus beraturan dapat diganti dengan kata kelajuan. Dengan demikian, dapat juga kita definisikan, gerak lurus beraturan sebagai gerak suatu benda pada lintasan lurus dengan kelajuan tetap.

Grafik perpindahan terhadap waktu GLB

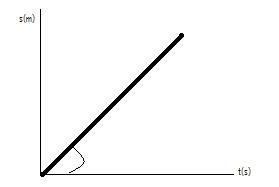
Grafik perpindahan terhadap waktu pada GLB ditunjukkan pada gambar di bawah ini. Tampak pada gambar bahwa grafik jarak/perpindahan (s) terhadap waktu (t) berbentuk garis lurus miring ke atas melalui titik asal koordinat O (0,0). Apabila ditinjau dari kemiringan grafik, maka tan α = v

Dengan demikian jika grafik jarak terhadap waktu (s-t) dari dua benda yang bergerak beraturan berbeda kemiringannya, maka grafik dengan sudut kemiringan besar menunjukkan kecepatan lebih besar.

Grafik kecepatan thdp waktu GLB

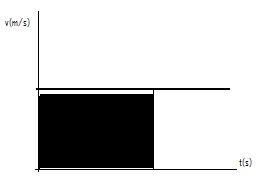
Grafik kecepatan terhadap waktu pada GLB ditunjukkan pada gambar di bawah ini. Tampak pada gambar bahwa grafik v-t berbentuk garis lurus mendatar. Bentuk ini menunjukkan bahwa pada GLB, kecepatan suatu benda selalu tetap untuk selang waktu kapanpun.

Hubungan jarak, waktu dan kecepatan dalam GLB

Pada gerak lurus beraturan kecepatan suatu benda selalu tetap. Jika diperhatikan kembali grafik v-t pada GLB, maka jarak/perpindahan (s) merupakan luas daerah yang dibatasi oleh v dan t.

Pada gambar di bawah ini tampak bahwa jarak/perpindahan sama dengan luas persegi panjang dengan panjang t dan lebar v.

Contoh Soal Untuk memahami konsep gerak lurus beraturan :
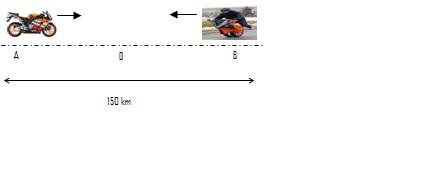
Dua sepeda motor bergerak saling mendekati pada lintasan lurus dengan arah berlawanan. Sepeda motor A bergerak ke barat dengan kecepatan tetap 30 km/jam, sedangkan sepeda motor B bergerak ke timur dengan kecepatan 45 km/jam. Sebelum bergerak, kedua sepeda motor terpisah sejauh 150 km.
(a). kapan dan dimana kedua sepeda motor berpapasan?
(b). tentukan jarak tempuh kedua sepeda motor saat berpapasan menggunakan grafik v-t tersebut.

(a). Misalkan kedua sepeda motor berpapasan di titik O. Dari gambar di atas diperoleh AO + BO = 150 km atau 150 km = 30km/jam.t + 45km/jam.t, sehingga diperoleh

t = 150 km/75 km/jam = 2 jam.

Jadi AO = 30 km/jam.2 jam = 60 km, sedangkan BO = 45 km/jam.2 jam=90 km
Kesimpulan, kedua sepeda motor berpapasan setelah bergerak selama 2 jam. Tempat  berpapasan adalah setelah sepeda motor A bergerak ke arah barat sejah 60 km atau setelah sepeda motor B bergerak ke arah timur sejauh 90 km.

(b). Jarak tempuh sepeda motor A = luas bangun A = panjang X lebar = 2 jam X 30 km/Jam = 60 km Jarak tempuh sepeda motor B = luas bangun B = panjang X lebar = 2 jam X 45 km/jam = 90 km

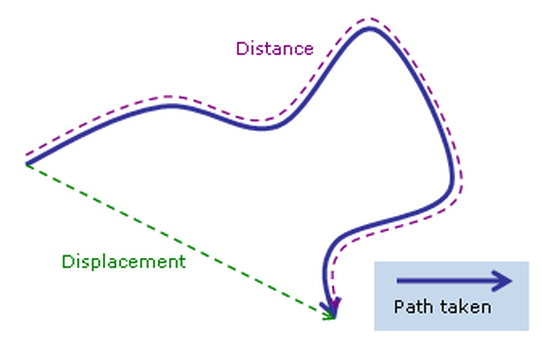
Ayo Sekarang Uji kompetensi Anda tentang Pemahaman konsep jarak dan perpindahan dengan mencoba latihan di bawah ini.

Sebuah mobil mengitari suatu arena balap berbentuk lingkaran.  Mobil bergerak mengitari sirkuit balap dari tempat start sebanyak dua kali dan akhirnya kembali ke tempat semula. Jika diameter sirkuit 1,0 km hitunglah (a) jarak yang ditempuh mobil, (b) perpindahan yang dialami mobil.

Contoh Pemahaman Konsep Kelajuan dan Kecepatan : 

Sebuah bus bergerak dari kota P ke kota Q sepanjang 400 m, kemudian bus melanjutkan perjalanan ke kota R sepanjang 300 m selama 0,5 jam.  Tentukan (a) laju rata-rata bus, (b) kecepatan rata-rata bus selama bergerak dari Kota P ke kota R.

Istilah Kinematika Rotasi

Kecepatan Sudut

Di dalam fisika, kecepatan sudut adalah besaran vektor (lebih tepatnya, vektor semu) yang menyatakan frekuensi sudut suatu benda dan sumbu putarnya. Satuan SI untuk kecepatan sudut adalah radian per detik, meskipun dapat diukur pula menurut derajat per detik, rotasi per detik, derajat per jam, dan lain-lain. Ketika diukur dalam putaran per waktu (misalnya rotasi per menit), kecepatan sudut sering dikatakan sebagai kecepatan rotasi dan besaran skalarnya adalah laju rotasi. Kecepatan sudut biasanya dinyatakan oleh simbol omega (Ω atau ω). Arah vektor kecepatan sudut adalah tegak lurus dengan bidang rotasi, dalam arah yang biasa disebut kaidah tangan kanan

Kecepatan sudut suatu partikel

Dimensi dua : Kecepatan sudut suatu partikel pada P relatif terhadap titik asal O ditentukan oleh komponen tangensial dan normal vektor kecepatan v. Kecepatan sudut suatu partikel di dalam bidang dua dimensi adalah yang paling mudah dipahami. Seperti yang ditunjukkan pada gambar di kanan (biasanya menyatakan ukuran sudut φ dan θ di dalam radian), jika garis dilukiskan dari titik asal (O) ke partikel yang dimaksud (P), maka vektor kecepatan (v) partikel akan memiliki komponen sepanjang jari-jari (komponen jari-jari, v∥) dan komponen yang tegak lurus dengan jari-jari (komponen silang jari-jari, v). Tetapi, harus diingat bahwa vektor kecepatan dapat juga diuraikan menjadi komponen tangensial dan normal.

Gerak radial (gerak memancar) tidak menghasilkan perubahan jarak partikel terhadap titik asal; sehingga untuk menentukan kecepatan sudut, komponen sejajar (radial) dapat diabaikan. Oleh karena itu, rotasi sepenuhnya dihasilkan oleh gerak tangensial (seperti yang terjadi pada partikel yang bergerak pada lingkaran), dan kecepatan sudut sepenuhnya ditentukan oleh komponen tegak lurus (tangensial).

Dapat dilihat bahwa laju perubahan kedudukan sudut suatu partikel adalah berhubungan dengan kecepatan silang jari-jari berdasarkan

Di dalam dimensi dua kecepatan sudut hanyalah nilai atau bilangan yang tak-berarah. Bilangan yang tak-berarah adalah skalar atau skalar semu, perbedaannya adalah skalar tidak mengubah tanda sumbu x dan y (atau dibalik), sedangkan skalar semu mengubah. Sudut sebagaimana halnya kecepatan sudut adalah contoh skalar semu. Arah positif rotasi diambil, berdasarkan perjanjian, sebagai arah menuju sumbu y dari sumbu x. Jika sumbu-sumbu itu dipertukarkan, tetapi rotasi tidak dibalik, maka tanda sudut rotasi, dan oleh karenanya pula kecepatan sudut akan berubah.

Adalah penting untuk mengetahui bahwa kecepatan sudut skalar semu suatu partikel bergantung kepada pilihan titik asalnya.

Percepatan Sudut

Percepatan sudut adalah laju perubahan kecepatan sudut terhadap waktu. Di dalam satuan SI, percepatan sudut diukur dalam radian per detik kuadrat (rad/s2), dan biasanya dilambangkan oleh abjad Yunani Alfa (α).

Percepatan sudut dapat didefinisikan sebagai:
ω = aT/r
di mana ω adalah kecepatan sudut, aT adalah percepatan tangensial linear, dan r adalah jarak dari titik nol sistem koordinat yang mendefinisikan θ dan ω ke titik yang dimaksud.

Percepatan tak-konstan Untuk setiap torsi tak-konstan, percepatan sudut suatu benda akan berubah seiring waktu. Persamaan yang ada menjadi persamaan diferensial, bukan nilai konstan. Persamaan diferensial ini disebut sebagai persamaan gerak sistem dan dapat secara utuh menjelaskan gerak benda. Cara ini juga merupakan yang terbaik untuk menghitung kecepatan sudut.

Istilah Kinematika Linear

Posisi, Jarak dan Perpindahan

Posisi
Posisi adalah kedudukan suatu obyek dari suatu acuan yang diambil. Acuan bisa diambil dimana saja dan ditentukan dari awal. Misalkan pada gambar dibawah, acuan terletak pada x = 0. Posisi balok pada gambar tersebut ada di x > 0. Bisa dimana saja, mungkin di x = 2 atau x = 5,6 atau dimana saja asalkan x bernilai positif.

Posisi adalah besaran vektor karena posisi memiliki besar dan arah.

Jarak
Jarak adalah lintasan suatu obyek selama obyek tersebut bergerak.

Perpindahan
Perpindahan sebuah partikel didefinisikan sebagai perpindahan posisi dimana perpindahan posisi tersebut haruslah merupakan JARAK TERPENDEK. Mari kita gunakan gambar diatas. Jika pada keadaan awal benda terletak pada x = 0, lalu pada waktu tertentu benda berada pada x = 3, maka perpindahan dari partikel tersebut adalah 3.

Perbedaan Jarak dan perpindahan terlihat dari sini

Dari gambar ditas, garis biru menunjukkan lintasan yang dilalui oleh sebuah partikel.
Garis merah merupakan JARAK dari partikel tersebut.
Garis hijau merupakan PERPINDAHAN dari partikel tersebut.

Secara umum, perpindahan dapat dirumuskan menjadi:

delta r menunjukkan perpindahan
rt menunjukkan posisi akhir benda
ro menunjukkan posisi  awal benda

Kecepatan dan Kelajuan

Kecepatan (velocity)
Kecepatan adalah besaran vektor yaitu besaran yang memiliki besar dan arah. Kecepatan dapat didefinisikan sebagai perubahan posisi sebagai fungsi waktu. Definisi ini didapat dari hasil diferensial perpindahan sebagai fungsi waktu.

Rumus kecepatan sesaat dapat dirumuskan menjadi :

V adalah kecepatan
delta d adalah perpindahan
t adalah waktu pada saat peninjauan

Kecepatan rata-rata dapat dirumuskan menjadi :

v adalah kecepatan rata-rata
delta x adalah perpindahan
delta t adalah waktu selama perpindahan tersebut

Kelajuan (speed)
Kelajuan adalah besaran skalar. Kelajuan pun dapat didefinisikan sebagai perubahan jarak sebagai fungsi waktu. Sama seperti kecepatan, kelajuan dapat dibedakan menjadi kelajuaan sesaat dan kelajuan rata-rata.

Rumus kelajuan sesaat adalah :

Speed adalah kelajuan
distance adalah jarak yang ditempuh
time adalah waktu pada saat tertentu

Rumus kelajuan rata-rata adalah :

sama seperti kelajuan sesaat hanya
delta t merupakan waktu yang dibutuhkan untuk menempuh jarak tersebut

Percepatan

Percepatan adalah laju perubahan kecepatan terhadap fungsi waktu. Percepatan merupakan hasil diferensial pertama dari kecepatan dan hasil turunan kedua dari perpindahan. Percepatan adalah besaran vektor. Karena perccepatan adalah fungsi waktu, maka terdapat 2 jenis percepatan dikaitkan dengan fungsi waktu yaitu percepatan sesaat dan percepatan rata-rata.

Percepatan sesaat  dapat dirumuskan :

Percepatan rata-rata dapat dirumuskan :

Sejarah Gerak Linear

Lebih dari 2000 tahun yang lalu, orang Yunani telah mempelajari beberapa ide dalam fisika seperti yang kini kita pelajari. Diantaranya, Aristoteles adalah salah satu filsuf dan ilmuwan yang terbesar di Yunani, ia kemudian menjelaskan fenomena gerak dengan membuat klasifikasi. Aristoteles membagi gerakan dalam dua tipe: gerakan alami dan gerakan gangguan.

Gerakan alami diduga berasal dari “sifat” benda. Dalam pandangan Aristoteles, setiap benda dalam alam semesta memiliki tempat tertentu, yang ditentukan oleh sifat ini; setiap benda yang tidak berada dalam tempat yang seharusnya akan “bergerak” untuk pergi ke tempat tersebut. Berada di bumi, benda terbuat dari tanah liat akan jatuh ke tanah; benda yang terbuat dari udara seperti asap akan naik ke atas; benda yang terbuat dari campuran tanah dan udara namun didominasi bumi, seperti bulu akan jatuh ke tanah namun tidak secepat benda yang terbuat dari tanah liat. Benda yang lebih besar akan bergerak lebih cepat. Karena itu, benda dipercayai jatuh dengan kecepatan proporsional dengan berat: makin berat sebuah benda, makin cepat benda akan jatuh ke tanah.

Gerakan alami dapat bergerak lurus ke atas atau ke bawah, dalam kasus untuk semua beda di bumi, namun dapat juga berbentuk lingkaran, seperti dalam kasus untuk benda-benda di langit. Tidak seperti gerakan ke atas dan ke bawah, gerakan melingkar dilihat sebagai gerakan tanpa awal dan akhir, berulang sendiri tanpa perubahan.

Gerakan gangguan, ditimbulkan dari gaya mendorong atau menarik. Seseorang mendorong sebuah kereta atau mengangkat sebuah benda mengakibatkan gerakan. Angin menimbulkan gerakan terhadap kapal laut. Hal mendasar tentang gerakan gangguan adalah disebabkan oleh penyebab luar dan diberikan kepada benda; benda bergerak bukan karena dirinya, tetapi karena didorong atau ditarik.

Konsep gerakan gangguan memiliki beberapa kesulitan, karena dorongan dan tarikan yang mengakibatkannya tidak selalu terlihat. Sebagai contoh, sebuah busur menggerakkan panah sampai panah meninggalkan busur; setelah itu, penjelasan untuk gerakan panah memerlukan penjelasan tentang pendorong yang lain selain busur. Maka, dibayangkan udara yang dipisahkan oleh panah menghasilkan efek menekan bagian belakang panah karena udara bergerak kembali, mencegah terjadinya kevakuman udara. Panah bergerak didorong melalui udara seperti sabun yang bergerak dalam air ketika bagian belakang sabun diperas, sehingga sabun terdorong maju.

Sebagai rangkuman, Aristoteles mengajarkan bahwa semua gerakan dihasilkan dari sifat benda bergerak atau dari dorongan ataupun tarikkan. Untuk benda pada posisi tertentu, maka tidak akan bergerak kecuali diberi gaya. Kecuali untuk benda-benda di langit, sifat normal benda-benda lainnya adalah diam.

Pandangan Aristoteles ini diikuti oleh banyak filsuf dan ilmuwan lainnya sampai 2000 tahun kemudian, yaitu bahwa bumi tidak bergerak. Baru pada klimaksnya seorang astronom Kopernikus memformulasikan teorinya tentang bumi yang bergerak. Kopernikus berargumen menggunakan data pengamatan astronominya bahwa bumi bergerak mengelilingi matahari. Lama ia tidak mempublikasikan teorinya tersebut, karena takut berbeda pandangan dengan yang lain dan masih ada keraguan karena ia belum dapat menghubungkan hubungan antara gerak bumi dan gerakan secara umum. Akhirnya, di hari terakhir hidupnya, bukunya dengan judul De Revolutionibus di cetak. Salinan pertama buku tersebut diperoleh pada hari kematiannya, 24 Mei 1543.

Baru kemudian Galileo, ilmuwan pada abad ke-16, yang memercayai pandangan Kopernikus tentang bumi yang bergerak. Ia membuktikannya dengan menunjukkan kesalahan ide Aristoteles tentang gerak. Hipotesis benda jatuh Aristoteles dengan mudah digugurkan Galileo. Ia melakukan percobaan dengan menjatuhkan benda dengan beragam berat dari puncak menara miring di Pisa dan membandingkan waktu kejatuhannya. Berlawanan dengan Aristoteles, ia menemukan batu yang beratnya dua kali lipat dibanding batu yang lain tidak jatuh lebih cepat dua kali lipat. Kecuali akibat gaya gesek dengan udara, Galileo kemudian menemukan bahwa benda dengan beragam berat, ketika dilepaskan pada waktu yang bersamaan, jatuh bersama dan menyentuh tanah pada waktu yang bersamaan. Suatu ketika, ia menunjukkan kepada kerumunan orang banyak untuk menyaksikan penjatuhan benda ringan dan berat dari puncak menara. Orang banyak yang melihat benda-benda tersebut jatuh ke tanah bersamaan, memarahi Galileo dan terus berpegang pada pandangan Aristoteles.

Galileo menguji hipotesis ini dengan bereksperimen dengan gerakan beragam benda pada bidang miring. Ia menyadari bahwa bola yang bergelinding ke bawah bidang miring bertambah cepat, sementara bola yang bergelinding ke atas bidang miring makin pelan. Dari hasil ini ia berargumen bahwa bola bergelinding di sepanjang bidang horizontal tidak akan bertambah cepat maupun berkurang cepat. Bola pada akhirnya akan berhenti bukan karena “sifatnya” namun karena gesekan. Ide ini didukung oleh pengamatan Galileo tentang gerak di sepanjang permukaan rata: ketika gesekan berkurang, maka semakin gerakan benda mendekati kecepatan konstan.

Ia kemudian beranggapan bahwa tanpa gesekan atau gaya berlawanan, benda yang bergerak horizontal akan terus bergerak.

Dugaan ini didukung oleh beragam eksperimen. Galileo meletakan kedua bidang miring saling berhadapan. Ia mengamati bahwa bola yang dilepaskan dari posisi diam pada puncak bidang miring menggelinding ke bawah kemudian ke atas bidang miring kedua sampai hamper mencapai tinggi mula-mula. Ia beranggapan bahwa hanya gesekan yang mencegahnya untuk sampai pada ketinggian yang tepat sama, untuk bidang yang rata, semakin bola mencapai tinggi yang sama. Lalu ia mengecilkan sudut dari bidang miring kedua. Kembali bola naik ke ketinggian yang sama, namun perlu menempuh jarak lebih jauh. Semakin sudut dikecilkan, menghasilkan hasil yang serupa; untuk mencapai ketinggian yang sama bola perlu menempuh jarak lebih jauh setiap kalinya. Kemudian ia bertanya, “Jika saya memiliki bidang horizontal, seberapa jauh bola harus menempuh untuk mencapai ketinggian yang sama.” Jawabannya sudah tentu “selamanya” karena bola tidak akan pernah mencapai tinggi mula-mula.

Galileo menganalisa hal ini dalam beberapa cara lain. Karena gerak menurun dari bola pada bidang pertama adalah sama untuk semua kasus, kecepatan awal bola ketika mulai bergerak menaiki bidang kedua adalah sama untuk semua kasus. Jika bola menaiki kemiringan yang tajam, bola segera mengalami penurunan kecepatan. Pada kemiringan yang landai, bola mengalami penurunan kecepatan lebih lambat dan menggelinding untuk waktu yang lebih lama. semakin kurang ketinggian kemiringan, semakin lambat bola mengalami penurunan kecepatan. Pada kasus ekstrim dimana tidak ada kemiringan, ketika bidang horizontal, bola tidak akan mengalami penurunan kecepatan. Dengan tidak adanya gaya penghambat, kecenderungan bola adalah bergerak terus tanpa melambat. Karakteristik dan benda bergerak untuk terus bergerak ia sebut inersia.
Konsep Galileo tentang inersia, menggantikan teori gerak Aristoteles. aristoteles tidak menyadari ide inersia karena ia gagal membayangkan benda yang bergerak tanpa gesekan. Kegagalan Aristoteles untuk menyadari gesekan sebagai gaya membuat perkembangan fisika tertunda 2000 tahun, sampai masa Galileo. Aplikasi konsep Galileo tentang inersia menunjukkan bahwa tidak ada gaya yang diperlukan untuk membuat bumi tetap bergerak. Sebuah jalan terbuka untuk Isaac Newton untuk menjelaskan pergerakan di alam semesta.